I am Martijn Grooten. I am a consultant, a researcher and a writer with a holistic view on digital security. I work with companies, non-profit organisations and at-risk individuals. This website serves as a portfolio for my expertise.
Update: I started working for Internews as a Digital Security Technologist in February 2022.
Consulting
I am a consultant on digital security, advising organizations, companies and individuals on a broad range of security-related topics, from helping to set up a security program to advising on product improvements.
Silent Push
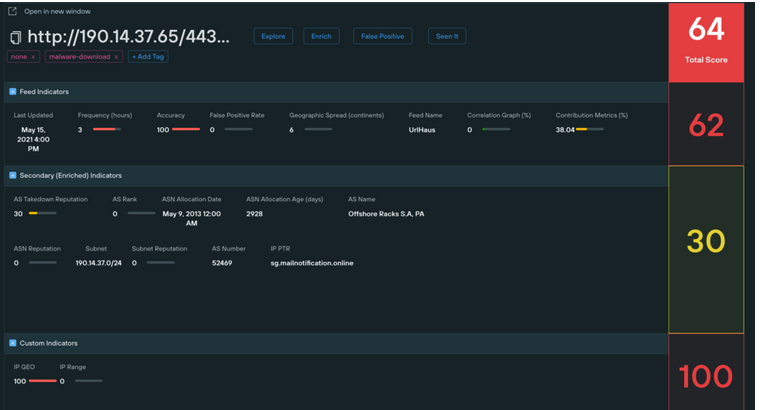
In 2021 and 2022, I worked as head of threat intelligence research for Silent Push, a startup working on detection-focused threat intelligence.
Cybersecurity Assessment Tool

I am part of a team at the Ford Foundation that developed this tool, that should help NGOs assess their digital security. A beta version was published in November 2020.
Coalition Against Stalkerware

I am a Special Advisor to this global coalition of security companies and non-profits that fights stalkerware: spy apps used in many abusive relationships.
Civilsphere Project

I am a fellow to the Civilsphere Project, which provides free solutions to NGOs, journalists and people at risk and which is linked to the Stratosphere IPS lab at the Czech Technical University in Prague.